Animasyonlu Grafikler Üzerinden Nedensel Çıkarımları Anlamak

Kontrol Etme, Eşleştirme, Araç değişkeni vb. yöntemleri anlamak

Bu yazı, Nick Huntington-Klein’in animasyonlu grafiklerle nedensel çıkarımları anlattığı sayfanın Türkçe yeniden anlatımıdır. Bu nedenle çok özgün şeyler yazmayacağım. Sadece üç şey yapacağım: 1) Ekstra bir bölüm eklemek, 2) Birebir çevirmek yerine Türkçe özetlemek, 3) Animasyonlu grafiklerdeki aşamaları Türkçe anlatmak

Sayfanın orjinalini bu linkten bulabilirsiniz: https://nickchk.com/causalgraphs.html#post-treatment-controls

Aynı zamanda Nick Huntington-Klein’in The Effect: An Introduction to Research Design and Causality kitabı internette erişime açıktır ve harika bir kitaptır. Lisans öğrencisiyseniz şimdiden okumanızı tavsiye ederim çünkü zamansız bir kitap. İçinde yazan şeyler yıllar sonra tekrar tekrar okunabilir.

Link: https://theeffectbook.net/

Giriş

Basit istatistik öğrenip ekonometri ve psikometri alanlarına geçtiğimizde bu alanlarda kullanılan yöntemler genellikle peş peşe sıralanıyor:

- Çok değişkenli OLS,

- Farkların farkı tahmincisi (Difference-in-Differences),

- Araç değişkenler (Instrumental Variables).

Bu yöntemlerin nasıl uygulanacağını ve bu yöntemleri kullanırken hangi varsayımlara başvurulduğunu öğreniyoruz; fakat çoğu zaman gerçekte ne yaptıklarını pek görmüyoruz.

Bu yazıda, gözlemsel verilerden nedensel etki çıkarmaya çalışan popüler yöntemleri, Nick Huntington-Klein’in hazırladığı animasyonlu grafiklerle anlatmaya çalışacağım. Böylece bu yöntemlerin “ne” yaptığını göreceğiz.

Öncelikle:

“Bir değişkendeki (A) varyasyonun başka bir değişken (B) tarafından açıklanması” ifadesi şu anlama geliyor:
B farklı değerler aldığında A’nın ortalamasına bakıyoruz. Örneğin, Alice’in boyu 163 cm, Bob’un boyu 183 cm, kadınların ortalama boyu 168 cm, erkeklerin ortalama boyu 175 cm olsun. Bu durumda Alice’in boyunun 168 cm’si, Bob’un boyunun 175 cm’si cinsiyet tarafından açıklanıyor. Geri kalan (163 – 168 = -5 cm) ve (183 – 175 = +8 cm) ise cinsiyetle açıklanamıyor.

Not:

Grafikler en iyi uygulama yöntemlerini göstermekten çok sezgisel bir anlayış vermek için tasarlanmış. Özellikle eşleştirme (matching) ve regresyon süreksizliği (RDD) örneklerinde sadece bir yöntemi veya zayıf bir versiyonunu gösteriyorlar.

Kontrol Etmek Ne Demek?

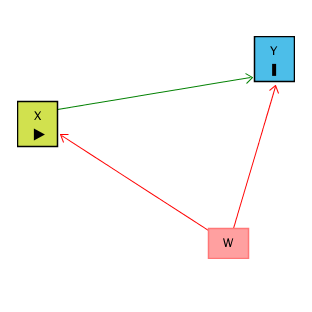
Bir araştırmada X’in Y üzerinde etkisi olup olmadığını anlamak istiyoruz. İlk bakışta sadece X ile Y arasındaki ilişkiye bakmak yeterli gibi görünebilir ama çoğu zaman değişkenler arasındaki ilişkileri incelemek bu kadar basit değildir çünkü X ve Y’yi aynı anda etkileyen üçüncü bir değişken (W) olabilir.

Bunu bir nedensel diyagramda şöyle görebiliriz:

• Asıl görmek istediğimiz yol X → Y (X’in Y üzerindeki doğrudan etkisi).

Fakat W hem X’i hem Y’yi etkiliyorsa, X ← W → Y diye bir “gizli” (back-door path) oluşur. Bu yol, gözlemlediğimiz X–Y ilişkisinin içine istenmeyen bir etki katar.

Örnek:

X = Eğitim düzeyi

Y = Gelir

W = Zekâ

Eğitimli insanların daha çok kazandığını gözlemledik. Bunun bir kısmı gerçekten eğitimden kaynaklanıyor ama bir kısmı da zeki insanların hem daha çok eğitim alma ihtimalinin yüksek olması hem de zekâları sayesinde zaten daha çok kazanabilmesi yüzünden ortaya çıkıyor. Yani gözlediğimiz ilişki salt eğitim etkisini yansıtmıyor. Bu sorunu nasıl çözebiliriz?

Burada ortaya çıkan gizli yolu kapatmak için W’yi kontrol etmek gereklidir. Başka bir deyişle, X ile Y arasındaki ilişkiye bakarken W’nin etkisini çıkarırız. Bunu da şu şekilde yaparız:

• X’in W tarafından açıklanan kısmını çıkarırız.

• Y’nin W tarafından açıklanan kısmını çıkarırız.

Geriye kalan X ve Y, W’den bağımsız hâle gelir. Böylece sadece X → Y etkisi kalır.

Özetle: Kontrol etmek, aynı W seviyesine sahip kişiler arasında X ile Y’nin ilişkisine bakmaktır. Bu sayede karıştırıcı (confounder) olan değişkenin etkisini ayırır ve daha doğru bir nedensel yorum yaparız.

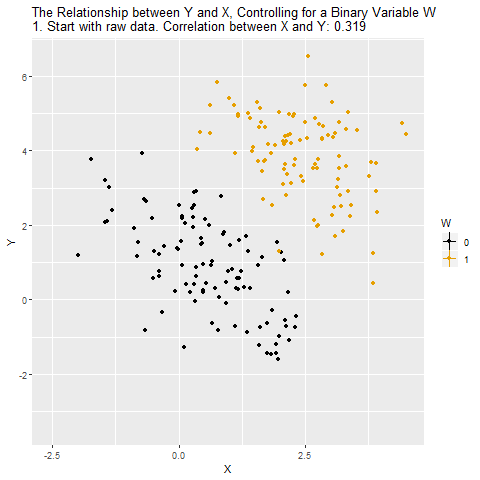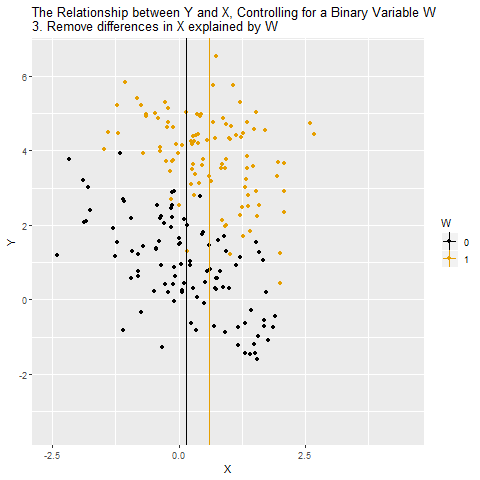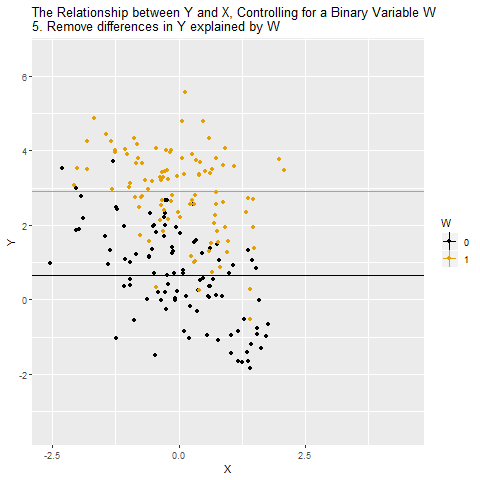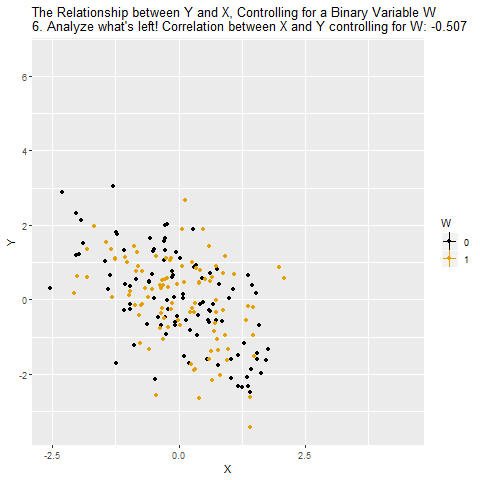
Aşağıdaki GIF’i okuyalım.

Başlangıçta grafikte X ve Y arasındaki ham ilişki gösteriliyor (GIF’teki 1, 2 ve 3 şeklinde devam edene aşamalara dikkatli bakın). Burada W adında ikili (0 veya 1) bir değişken var ve siyah ile turuncu noktalar bu iki farklı W değerini temsil ediyor. İlk bakışta X ile Y arasında pozitif bir korelasyon var (0.319).

Bu ilişki iki şeyin karışımı:

• X’in Y üzerindeki gerçek etkisi (ilgilenilen kısım).

• W’nin hem X’i hem Y’yi etkilemesinden doğan sahte ilişki (istemediğimiz kısım).

GIF’te şu işlemler yapılıyor:

Önce X’in W tarafından açıklanan kısmı çıkarılıyor (2 ve 3)

Sonra Y’nin W tarafından açıklanan kısmı çıkarılıyor (4 ve 5)

Yani, her iki değişkenden de W’nin payı temizleniyor ve inceleniyor (6)

Böylece W üzerinden ortaya çıkan gizl yol (X ← W → Y) kapanıyor ve elimizde sadece X → Y ilişkisi kalıyor. Yani artık korelasyon, W’nin etkisinden arındırılmış hâlde gerçekten X’in Y üzerindeki etkisini gösteriyor. Kontrol etmek dediğimiz şey aslında X ve Y’den W’nin payını çıkarmak ve onları aynı W seviyesinde kıyaslamaktır. Böylece gözlemlenen ilişkiyi daha güvenilir biçimde nedensel yorumlayabiliriz.

Eşleştirme (Matching) Ne Demek?

Bir işlemin/uygulamanın (Treatment) Y üzerindeki etkisini ölçmek istediğimizde, en basit yol Treatment alanlarla almayanları karşılaştırmak gibi görünebilir. Yani sadece “İşlemin/Treatmentın uygulandığı şehirler ne kadar büyüdü, kontrol şehirleri ne kadar büyüdü?” diye bakarız. Fakat bu yaklaşım yanıltıcı olabilir çünkü İşlem ile Y arasındaki ham ilişki genellikle başka faktörlerden de etkilenir.

Buradaki temel sorun, İşlem’i uygulayan ve uygulamayan grupların birbirine benzememesidir. Eğer İşlem ile Y arasında başka bir değişken (X) ortak olarak rol oynuyorsa, bu durumda gizli yol (back-door path) oluşur. Yani Y üzerindeki farklar yalnızca İşlemin etkisinden değil, aynı zamanda X’in hem İşlemi’i hem de Y’yi etkilemesinden kaynaklanır

Somut bir örneği inceleyelim:

Treatment: 2014’te yol altyapısını geliştiren şehirler; Y: 2015’teki ekonomik büyüme oranı; X: 2014 öncesindeki büyüme eğilimi.

Burada gözlenen fark şudur: Yolunu geliştiren şehirler sonraki yıl daha hızlı büyümüştür. Bunun bir kısmı gerçekten yol yatırımlarının ekonomiyi canlandırmasından gelir ama bir kısmı da zaten önceden hızlı büyüyen şehirlerin bu yatırımları yapacak maddi imkânlara sahip olmasından gelir. Yani aslında gözlenen farkın tamamını yollara bağlamak hatalı olur.

İşte bu nedenle devreye matching (eşleştirme) yöntemi girer. Matching, Treatment alan şehirleri, sadece benzer X değerlerine sahip kontrol şehirleriyle karşılaştırmamızı sağlar. Yani “önceden aynı büyüme eğilimine sahip şehirler” arasında kıyaslama yaparız. Bu yaklaşım, Treatment ← X → Y gizli yolu kapatır ve geriye yalnızca Treatment → Y kalır.

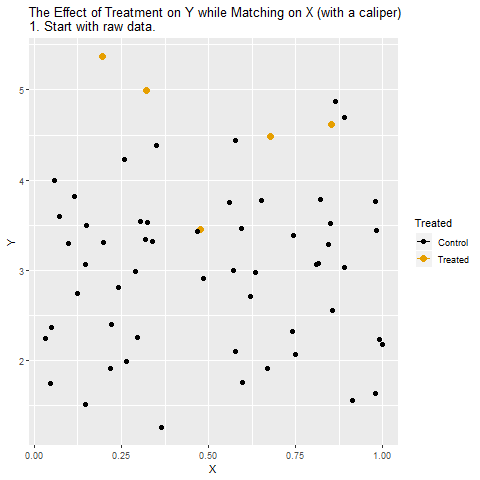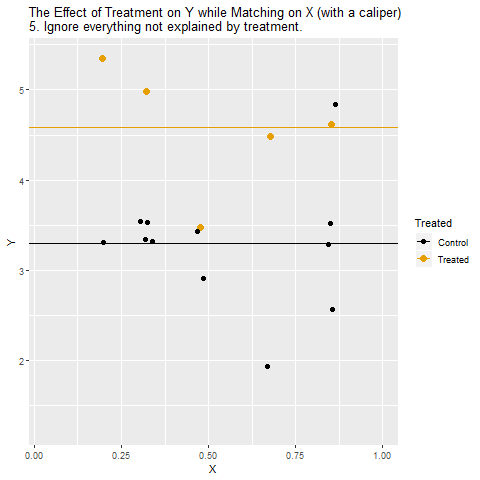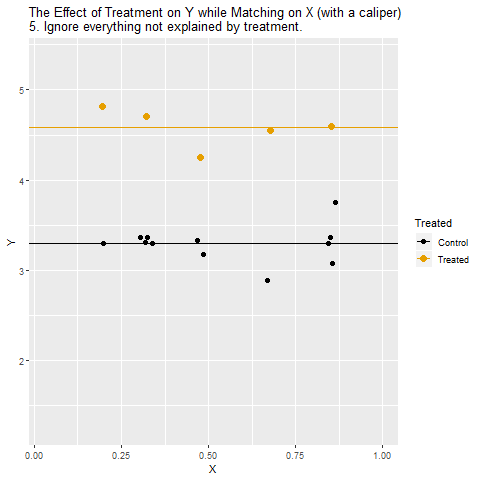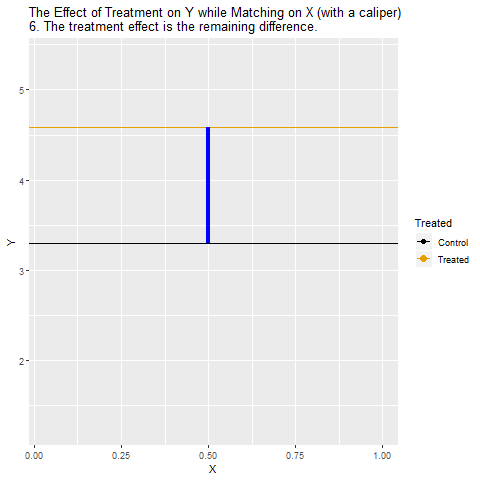
Aşağıdaki GIF üzerinden bakalım.

• Ham veriyle başlıyoruz: İlk karede ham veriyi görüyoruz. Turuncu noktalar Treatment alan gözlemleri, siyah noktalar ise kontrol grubunu temsil ediyor. Burada gözlenen farklar hem İşlemin gerçek etkisini hem de X’in karıştırıcı etkisini içeriyor.

• X üzerinden eşleştiriyoruz: Sonraki adımda Treatment grubundaki gözlemler, benzer X değerlerine sahip kontrol grubundaki gözlemlerle eşleştiriliyor. Böylece karşılaştırmalar “aynı X koşullarında” yapılabiliyor.

• Kötü eşleşmelerı çıkarıyoruz: Eşleştirmede benzer X değerine sahip uygun kontrol bulunamayan bazı Treatment gözlemleri eleniyor. Bu sayede daha adil bir kıyaslama zemini sağlanıyor.

• Eşleştirilmiş olanları kıyaslıyoruz: Artık her Treatment gözlemi yalnızca kendisine benzeyen kontrol gözlemleriyle karşılaştırılıyor. Böylece Treatment ← X → Y gizli yolu kapanıyor.

• Treatment/İşlem* etkisini ölçüyoruz: Bu eşleştirilmiş gruplardan elde edilen fark, İşlemin Y üzerindeki etkisini daha temiz biçimde yansıtıyor.

• Yorumluyoruz: Sonuçta elde edilen ilişki, X’in etkisinden arındırılmış, nedensel yoruma daha yakın bir etki ölçüsü oluyor.

Başka bir ifadeyle, matching yapıldığında gerçekleşen süreç şu şekildedir:

• İşlemin etkisini görmek isterken, X’in payını denk gruplar oluşturarak elimine ederiz.

• Karşılaştırma “aynı özelliklere sahip şehirler” üzerinden yapılır, tek fark yol yatırımı yapıp yapmamalarıdır.

Böylece gözlediğimiz ilişki nedensel yoruma daha çok yaklaşır. Matching, nedensel analizde en sık kullanılan yöntemlerden biridir çünkü sadece Treatment ile Control arasındaki farklara bakmak yerine, onları benzer özelliklere göre eşleştirir ve karşılaştırmayı adil bir zemine taşır. Bu yöntem, özellikle gözlemsel verilerde (deney yapamadığımız durumlarda) politikaların ya da işlemlerin etkisini ölçmek için çok önemlidir.

Araç Değişkeni (Instrumental Variable) Nedir?

X’in Y üzerinde etkisini ölçmek istiyoruz ama bu ilişkiyi doğrudan gözlemlemek yanıltıcı olabilir çünkü X ile Y arasındaki farklara aynı anda etki eden başka bir değişken (W) olabilir. Bu durumda gözlediğimiz ilişki iki parçadan oluşur:

• X → Y’nin gerçek etkisi (bizim öğrenmek istediğimiz kısım),

• W’nin hem X hem de Y üzerindeki etkilerinden gelen sahte ilişki (görmek istemediğimiz kısım).

Bu durumda X ile Y arasındaki ham korelasyon yanıltıcı olur çünkü gizli yol (X ← W → Y) açıktır.

İşte bu noktada araç değişken (instrumental variable, IV) devreye girer. Eğer elimizde X’i etkileyen ama Y üzerinde doğrudan bir etkisi olmayan bir değişken (Z) varsa, bu değişkeni “araç” olarak kullanabiliriz. Z’nin Y üzerindeki tek etkisi, X üzerinden geçer. Bu nedenle Z ile Y arasındaki ilişki W’den bağımsızdır. Böylece yalnızca Z’nin açıkladığı X kısmını kullanarak, X’in Y üzerindeki nedensel etkisini elde edebiliriz.

Örnek üzerinden düşünelim:

• X = Ebeveyn geliri

• Y = Çocuğun sağlığı

• W = Ebeveyn sağlığı (hem gelirle hem çocuk sağlığıyla ilişkili, yani gizli yolu açıyor)

• Z = Ebeveynlere çocukları için verilen bir sosyal yardım programı (ebeveynin gelirini artırıyor ama ebeveyn sağlığıyla hiçbir ilgisi yok).

Burada ebeveyn geliri ile çocuk sağlığı arasındaki ham ilişki karışık bir tablo sunar çünkü hem gelir hem sağlık aynı anda etkilidir. Fakat çocuklar için verilen sosyal yardım programı (Z) tamamen rastgele verildiği için ebeveyn sağlığıyla bağlantılı değildir. Z yalnızca geliri değiştirir. Dolayısıyla Z’nin açıkladığı gelir artışı kısmını izole ettiğimizde, bunun çocuk sağlığı üzerindeki etkisi saf bir şekilde X üzerinden gelmektedir.

Önemli nokta şudur:

• Kontrol etme yönteminde, X ve Y’den belirli bir değişkenin (örneğin W) açıkladığı kısmı çıkarırız ve geriye kalan kısımlarla inceleriz.

• Instrumental variables yönteminde ise tam tersini yaparız: X ve Y’nin sadece Z’nin açıkladığı kısmını alırız, geri kalan tüm varyasyonu atarız.

Yani kontrol etme, veriden istenmeyen kısmı temizlemeye çalışırken; araç değişken yöntemi, veriden yalnızca güvenilir kaynağı (Z’nin etkisini) çekip alır.

Sonuç olarak, eğer Z gerçekten iyi bir araçsa (Y’yi yalnızca X üzerinden etkiliyorsa), IV sayesinde X → Y’nin nedensel etkisini, W gibi karıştırıcıların bozucu etkisinden arındırılmış şekilde tahmin edebiliriz.

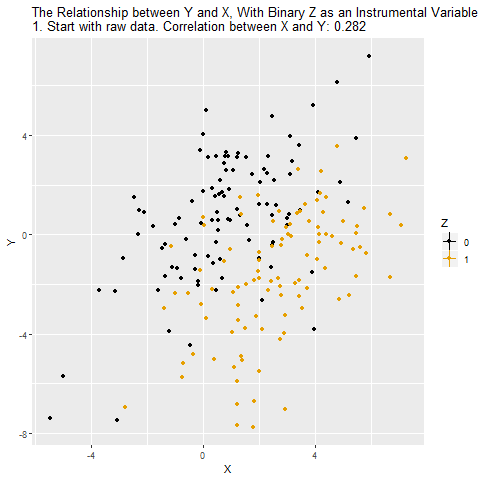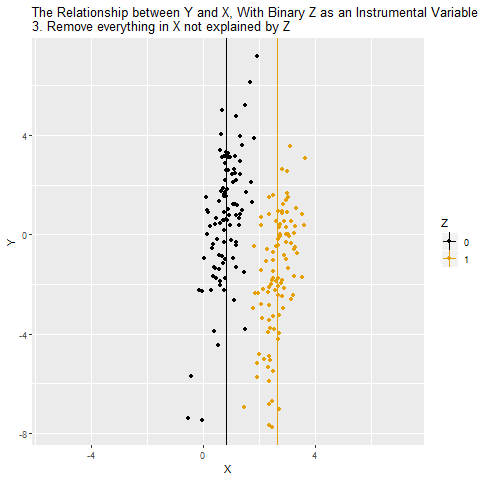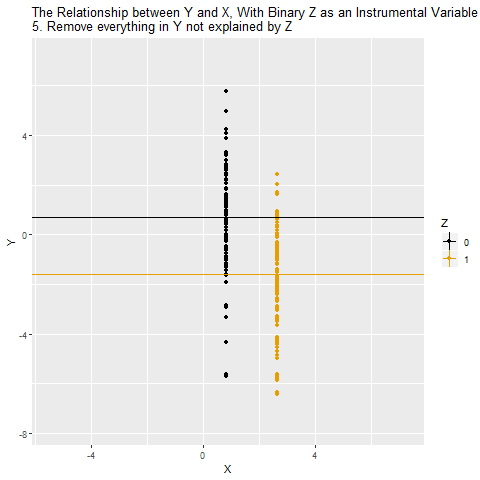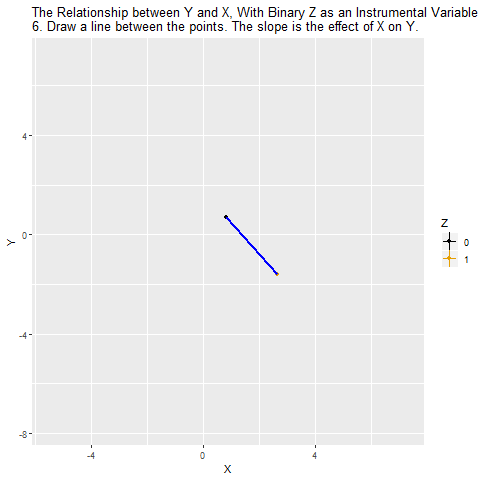
Aşağıdaki GIF’i okuyalım:

1. İlk karede X ile Y arasındaki ham ilişki gösteriliyor. Noktaların rengi Z’nin (araç değişken) iki değerini (0 = siyah, 1 = turuncu) temsil ediyor. Burada görülen korelasyon (0.282), X’in Y üzerindeki gerçek etkisini tam olarak yansıtmıyor çünkü karıştırıcı değişkenlerin (W) etkisi de işin içinde.

2. İkinci aşamada X’in Z tarafından açıklanan kısmı ortaya çıkarılıyor. Yani Z=0 ve Z=1 gruplarına göre X’teki sistematik farkları görüyoruz. Bu, X’in “araç değişkene bağlı varyasyonu” oluyor.

3. Üçüncü aşamada X değişkeni, “Z’nin açıkladığı kısım” ve “diğer her şey” diye ayrışıyor. IV mantığında yalnızca Z’nin açıkladığı bu temiz kısım kullanılıyor çünkü diğer kısımlar karıştırıcılarla ilişkili olabilir.

4. Dördüncü aşamada, Y sadece X’in Z tarafından açıklanan kısmıyla ilişkilendiriliyor. Burada gizli yol (X ← W → Y) kapanıyor çünkü Z’nin W ile bağlantısı yok.

5. Beşinci aşamada elde edilen ilişki, X’in Y üzerindeki nedensel etkisini temsil ediyor. Yani artık gözlenen korelasyon karıştırıcıların etkisinden arındırılmış hale geliyor.

6. Altıncı aşamada, IV yöntemi sayesinde yalnızca Z’nin açıklayabildiği X varyasyonu üzerinden Y’ye giden etkiyi ölçmüş oluyoruz. Bu da daha nedensel ilişki tahmini yapmamıza olanak tanıyor.

Sabit Etkiler (Fixed Effects) Yöntemi

X’in Y üzerindeki etkisini incelemek isterken karşılaştığımız en büyük sorunlardan biri, gözlemlediğimiz bireylerin (veya firmaların, şehirlerin, ülkelerin) kendilerine özgü, zaman içinde değişmeyen özellikleridir. Bu özellikler (bazen “görülmeyen heterojenlik” denir), hem X’i hem de Y’yi etkilediği için X ile Y arasındaki ilişkiyi bozabilir.

Böyle bir durumda gözlenen ilişki iki parçaya ayrılır:

1. X’in Y üzerindeki gerçek etkisi → ilgilendiğimiz kısım.

2. Birey/firmaya özgü sabit özelliklerin etkisi → istemediğimiz kısım.

Örnek üzerinden düşünelim:

X = CEO’nun eğitim düzeyi, Y = firmanın yıllık kârı olsun.

• Daha prestijli ve büyük firmalar hem daha kârlıdır hem de daha yüksek eğitimli CEO’lar seçer.

• Bu durumda “yüksek eğitimli CEO → daha çok kâr” ilişkisi aslında firmaya özgü (yani CEO’nun kendisi değil) özelliklerden kaynaklanıyor olabilir.

İşte Fixed Effects yöntemi burada devreye girer. Bu yöntem, farklı bireyleri birbirleriyle kıyaslamak yerine, aynı bireyin zaman içindeki değişimlerini karşılaştırır.

Başka bir deyişle, her firmayı kendi geçmişiyle kıyaslarız:

• Firma A’nın düşük eğitimli CEO’su olduğu yıllardaki kârı,

• Aynı firma A’nın yüksek eğitimli CEO’su olduğu yıllardaki kârı ile kıyaslanır.

Böylece firmaya özgü değişmeyen özellikler (sektör, coğrafya vb.) sabit kalır ve analizden “çıkarılmış” olur.

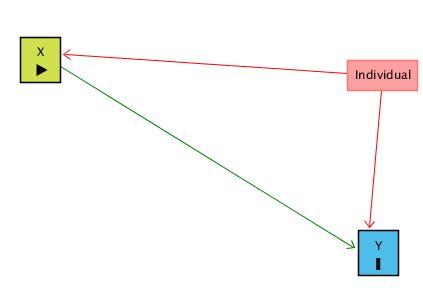
Birey/Firma sabit etkilerini (fixed effects) kullanarak, her bireyi birden fazla kez gözlemlediğimiz sürece, “Individual” üzerinden geçen gizli yolu kapatabiliriz. Buradaki fikir, X ile Y arasındaki ilişkiye her bireyin kendi içinde bakmaktır. Bunu başka bir şekilde söylemek gerekirse, her bireyin kim olduğunu “kontrol altına almış” oluruz. Bunu yaptığımızda, X ← Individual → Y yolu kapanır ve elimizde yalnızca X → Y kalır; bu da ilgilendiğimiz ilişkidir. Bireyi kontrol ettikten sonra, X ile Y arasındaki kalan ilişki nedenseldir (tabii tek gizli yolu Individual üzerinden geçiyorsa).

Peki X ile Y arasındaki ilişkiye bireyin kendi içinde nasıl bakabiliriz? Bunu kontrol ederek yaptığımız şey, X ve Y’nin bireysel kimlikler tarafından açıklanan kısımlarını çıkarmaktır. X ve Y’nin birey kimlikleriyle tahmin edilebilecek tüm kısımları çıkarılır, böylece bu arka kapı/gizli yol kapanmış olur ve X ile Y’yi sadece birey içi karşılaştırmalarla incelemiş oluruz.

Sabit etkiler modeli genellikle şu şekilde yazılır:

\(Yit​=αi​+βXit​+ϵit​ \)

• Yit​: birey/firmanın t dönemindeki çıktı değeri (örneğin kâr),

• Xit​: aynı bireyin/firmadaki bağımsız değişken (örneğin CEO eğitim düzeyi),

• αi: bireye özgü, zaman içinde değişmeyen sabit etki (örneğin firmanın genel kârlılık yapısı),

• β: X’in Y üzerindeki nedensel etkisi (bulmak istediğimiz),

• ϵit​: hata terimi.

Bu modelde αi​ sabit etkileri temsil eder. Tahmin sırasında bu sabit etkiler çıkarılır, yani bireylerin sabit özellikleri otomatik olarak kontrol altına alınır. Böylece analiz yalnızca zaman içindeki değişimlere dayanır.

Bir de aşağıdaki GIF üzerinden bakalım:

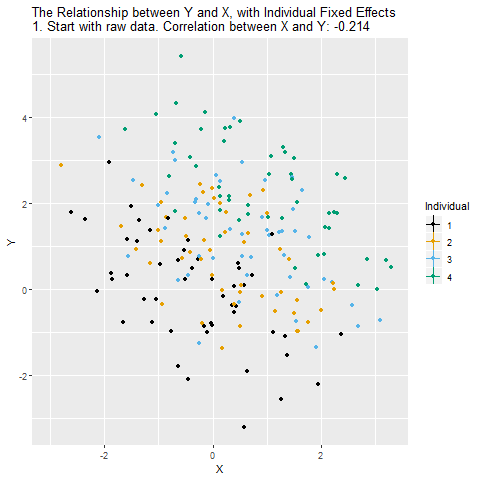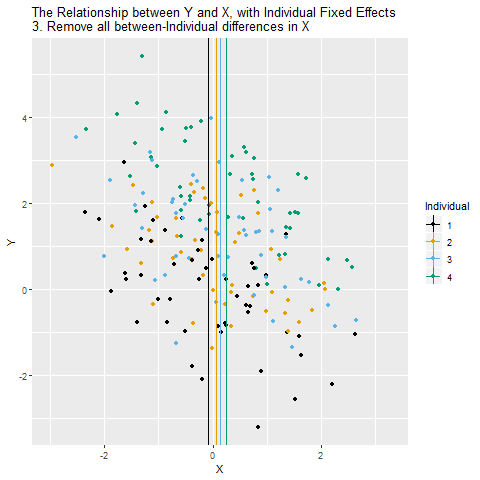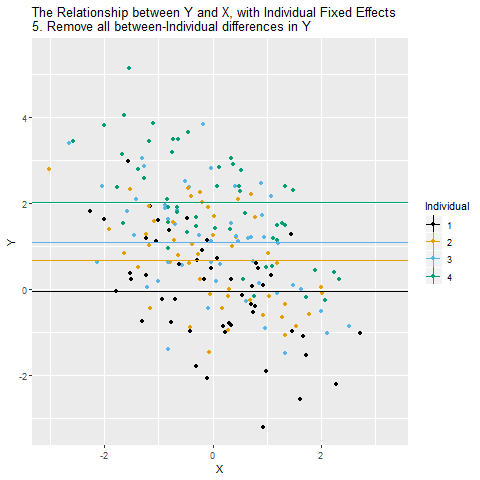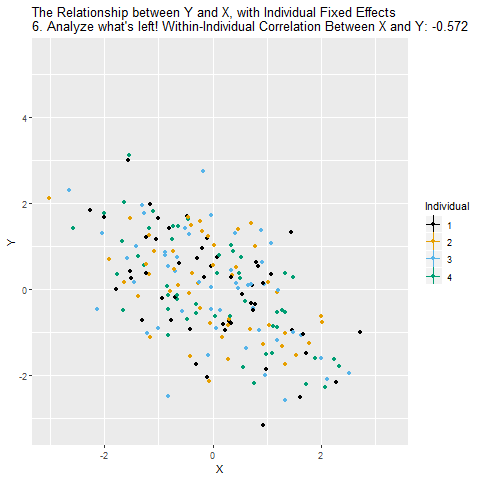
1. Grafikte X ve Y arasındaki ilişki gösteriliyor. Farklı renkler farklı bireyleri (örneğin firmaları) temsil ediyor. Bu aşamada ilişki hem gerçekten X’in Y üzerindeki etkisini hem de bireylere özgü sabit özellikleri (örneğin sektör, büyüklük, coğrafi konum gibi hiç değişmeyen şeyleri) içeriyor. Yani gördüğümüz ilişki yanıltıcı olabilir.

2. Her bireyin zaman içindeki ortalama X ve ortalama Y değeri düşünülüyor. Bu, bireyler arasındaki sabit farklılıkları gösteriyor. Örneğin bazı firmalar sürekli daha kârlı, bazıları sürekli daha az kârlı olabilir. Bu farklılıklar X–Y ilişkisinin içinde gizli duruyor.

3. Her birey için “o bireyin ortalama X değerini” çıkarıyoruz. Böylece X yalnızca zaman içinde değişen kısmıyla kalıyor. Yani artık X’in içinde bireylere özgü sabit farklar yok.

4. Aynı şekilde, Y’den de her bireyin kendi ortalama değerini çıkarıyoruz. Böylece Y de sadece bireyin zaman içinde gösterdiği değişimlerden oluşuyor, bireyler arası sabit farklar temizlenmiş oluyor.

5. Artık elimizde sadece “birey içindeki değişimler” var. Yani aynı bireyin X’i arttığında Y’si nasıl değişiyor sorusunu yanıtlıyoruz. Bireyler arası farklılıkları hesaba katmıyoruz. Bu yeni ilişki sabit etkiler (fixed effects) ile elde edilen tahmin oluyor.

6. Sonuçta, bireylerin kim olduklarını ve onların değişmeyen özelliklerini kontrol etmiş oluyoruz. Böylece X ile Y arasındaki ilişkiyi daha doğru ve nedensel bir şekilde ölçebiliyoruz. Tabii bunun çalışması için aynı bireyi birden fazla zaman gözlemlememiz (panel veri) gerekiyor. Ayrıca birey içinde zamanla değişen başka etkenler varsa, bunları da ayrıca düşünmek gerekebilir.

Farkların farkı tahmincisi (Difference-in-Differences) Nedir?

Bir grup insana (Treated, işlem uygulanmış) belirli bir zamanda yeni bir işlem uygulanıyor. Bu grubu hem öncesinde (Before) hem de sonrasında (After) gözlemleyebiliyoruz. Amacımız, işlemin Y üzerindeki etkisini ölçmek.

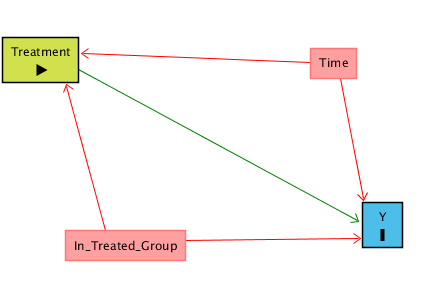
İlk akla gelen yöntem, Treated grubunda işlem öncesi ve sonrası arasındaki farkı almaktır. Ama sorun şu: Y, aynı dönemde herkeste artmış olabilir. Yani gözlenen değişim hem işlemin etkisini hem de zamanın genel etkilerini içerir. Bu durumda “zaman” bir arka kapı yolu veya gizli yol (back-door path) yaratır:

• İstediğimiz yol: Treatment/İşlem → Y

• İstemediğimiz yol: Treatment ← Time → Y

Burada tek başına “zamanı kontrol etmek” de işe yaramaz, çünkü Treated grubunda zaman ile treatment tamamen örtüşür: Önce = İşlem yok, Sonra = İşlem var. Bu durumda Treatment ile Time birbirinden ayrılamaz.

Örneğin, Treatment belirli bir ofisin bölmeli ofisten açık ofise geçmesi olsun ve Y de verimlilik olsun. Geçiş 1 Ocak 2017’de yapılıyor. Bu durumda Before Treatment 2016 yılı, After Treatment ise 2017 yılı olabilir. Fakat 2016 ve 2017 yılları arası ekonomi iyileşmiş olabilir, bu yüzden verimlilikteki artışın açık ofise geçişle hiçbir ilgisi olmayabilir.

Bu durumda, işlem uygulanan grupta (Treated) Y’nin işlem öncesi ve sonrası farkı iki şeyi yansıtacaktır:

1. İşlemin Y üzerindeki etkisi (ilgilendiğimiz kısım),

2. Y’nin, İşlemle ilgisi olmayan nedenlerle, zaman içinde değişmiş olabileceği etkiler (ilgilenmediğimiz kısım).

Zaman (Time), İşlem’den Y’ye bir gizli yol oluşturur. Yani İşlemden Y’ye, 1) İşlem → Y yolu üzerinden (istediğimiz yol), veya 2) İşlem ← Zaman → Y yolu üzerinden (istemediğimiz yol) gidilebilir.

Daha da kötüsü, eğer sadece İşlem uygulanmış/Treatment grubuna bakarsak, Zaman değişkenini kontrol ederek bu arka kapıyı/gizli yolu kapatamayız çünkü Zaman, İşlemi (Treatment) tamamen öngörebilir. Dolayısıyla, İşlemin, Zaman tarafından açıklanan tüm kısımlarını çıkarırsak elimizde hiçbir şey kalmaz.

Peki ne yapabiliriz? Hiç işlem uygulanmayan bir Kontrol grubu ekleyebiliriz (örneğimizde, 2016 ve 2017 boyunca bölmeli ofisi koruyan bir başka ofis). Bu, Zaman’ı kontrol etmemizi sağlar; lâkin bu kez de başka bir gizli yol sorunu ortaya çıkar çünkü Kontrol ve Treated (İşlem Uygulanmış)grupları birbirinden farklı olabilir.

• Treatment ← In_Treated_Group (Treated vs Control) → Y

Yani Treated ve Control grupları zaten farklı olabilir:

Difference-in-Differences mantığı şu şekilde işliyor:

• Önce Treated/İşlem Uygulanan grubunun Y’deki Before–After farkını hesaplarız.

• Sonra Kontorl grubunun Y’deki Before–After farkını hesaplarız.

• İki farkı birbirinden çıkarırız: (Treated’in farkı – Control’ün farkı).

Böylece:

• Kontrol grubunun Before–After farkı çıkarıldığı için zamanın genel etkisi kontrol edilmiş olur.

• Treated ile Kontrol kıyaslandığı için gruplar arasındaki sabit farklılıklar da kontrol edilmiş olur.

Sonuçta geriye sadece işlemin (Treatment’in) Y üzerindeki nedensel etkisi kalır.

GIF üzerinden bakalım:
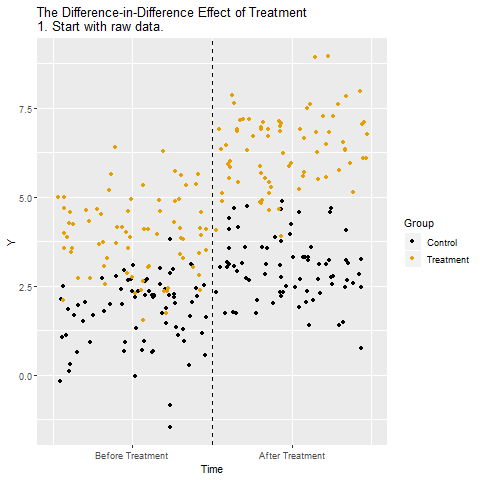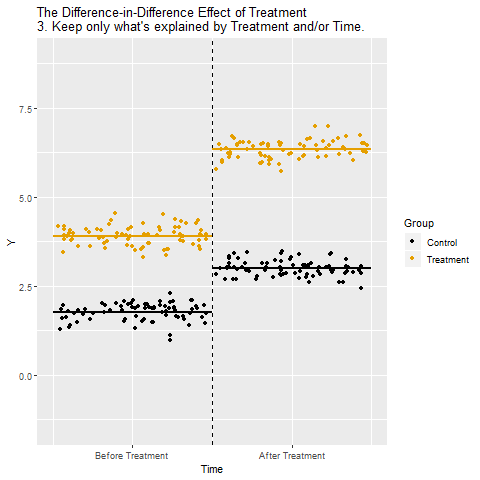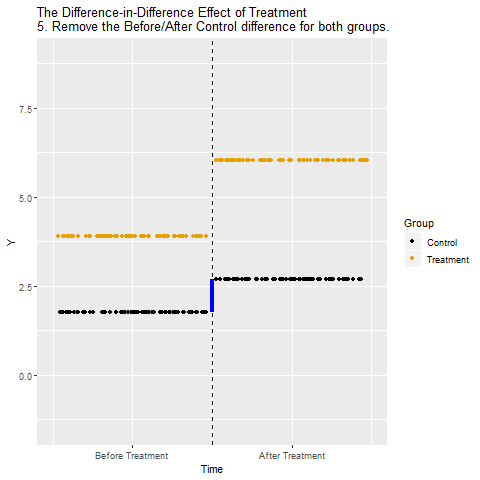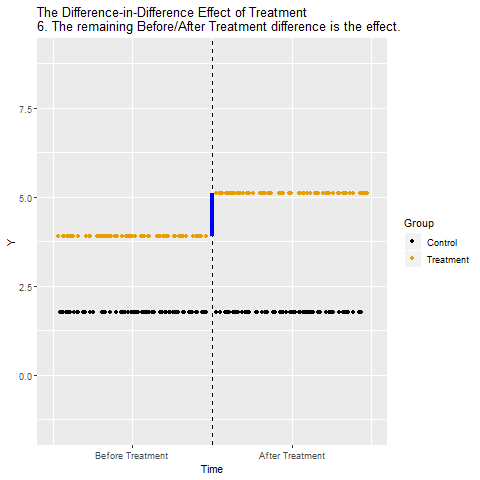
Grafikte deney (turuncu) ve kontrol grubu (siyah) var. İki grup da “İşlem Öncesi” ve “İşlem Sonrası” dönemlerinde gözleniyor. Bu ham farklar, hem işlemin etkisini hem de zamana bağlı genel değişimleri içeriyor.

İşlem grubundaki değişim: İşlem grubunda Önce → Sonra farkına bakılıyor. Bu fark hem işlemin etkisini hem de döneme özgü (zamanın) değişimi kapsıyor.

Kontrol grubundaki değişim: Kontrol grubunda Önce → Sonra farkı hesaplanıyor. Burada işlem uygulanmadığı için fark yalnızca zamana bağlı genel değişimden kaynaklanıyor.

İşlem Uygulanan gruptaki değişim ile Kontrol grubundaki değişim yan yana konuluyor. Böylece işlemin etkisi ile zamanın etkisi birbirinden ayrıştırılmaya hazırlanıyor.

Difference-in-Differences (Farkların farkı)
Kontrol/İşlem grubu farklları çıkarılıyor:
(İşlem Uygulanan Sonra – İşlem Uygulanan Önce) – (Kontrol Sonra – Kontrol Önce).
Böylece zamanın etkisi elimine ediliyor.

Yorum:

Sonuçta elde edilen değer, işlemin (treatment’in) Y üzerindeki net, nedensel etkisini gösteriyor. Zamanın ve gruplar arası sabit farklılıkların etkisi temizlenmiş oluyor.

Regresyon Süreksizliği (Regression Discontinuity)

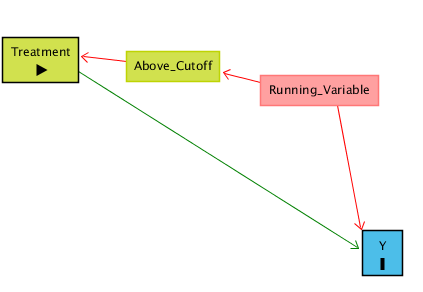
Bir işlemin (Treatment) Y üzerinde etkisi olup olmadığını ölçmek istiyoruz ama Treatment hiçbir şekilde rastgele dağılmamış/rastgele verilmemiş; bir İşleyiş Değişkeni (Running Variable) üzerinden belirleniyor. Eğer bu değişken belirli bir eşik değerinin (Cutoff) üstündeyse Treatment alınıyor, altındaysa alınmıyor.

Buradaki sorun şu: İşleyiş Değişkeni (RV) hem Treatment’i (işlemi) belirliyor, hem de kendi başına Y’yi etkiliyor olabilir. Yani gözlenen ilişki iki şeyin karışımıdır:

1. Treatment → Y (görmek istediğimiz etki),

2. Running Variable → Y (istemediğimiz, karıştırıcı etki).

Treatment hem doğrudan Y’yi etkiliyor, hem de Running Variable üzerinden dolaylı bir yol var:

Örnek üzerinden düşünelim.

Örnek:
Diyelim ki bir şehirde öğrenciler için Üstün Yetenekliler Programı var. Bu programa kabul edilmek (Treatment), öğrencinin gelecekte üniversiteye girme ihtimalini (Y) artırabilir. Fakat programa kabul edilmek, öğrencilerin sınavdan aldığı puana (Running Variable) göre belirleniyor.

Kural şu:

• Sınav puanı 90 ve üzeri olanlar programa kabul ediliyor (işlem gerçekleşiyor).

• 90’ın altındakiler ise programa giremiyor (işlem gerçekleşmiyor).

Buradaki sorun şudur:

• Zaten yüksek puan alan öğrenciler, programa girseler de girmeseler de, üniversiteye gitme ihtimali daha yüksektir.

• Yani gözlenen farkın bir kısmı programın etkisinden değil, yüksek puanlı öğrencilerin zaten başarılı olmasından kaynaklanır.

Tam da bu yüzden 90 puan eşiğinin hemen altında ve hemen üstünde kalan öğrenciler karşılaştırılır. Örneğin:

• 89 puan alan bir öğrenci programa giremez.

• 90 puan alan bir öğrenci programa girer.

Aradaki fark sadece 1 puandır, yani öğrencilerin başarı düzeyleri neredeyse aynıdır. Bu durumda üniversiteye gitme oranlarındaki fark, büyük ölçüde programın etkisinden kaynaklanır.

Dolayısıyla, eşik değerin (cutoff) hemen çevresinde yapılan karşılaştırma bize programın Y üzerindeki nedensel etkisini verir.

Çözüm: Eşik Değeri çevresine odaklanmak

Sınav puanı 90 eşiğinde, öğrencilerin programa kabul edilip edilmemesi neredeyse rastgele sayılabilir:

• 89 alan öğrenci ile 90 alan öğrenci arasında gerçek bir yetenek farkı yoktur ama sadece biri programa girer, diğeri giremez.

Bu durumda, iki öğrenci grubu arasındaki fark bize programın üniversiteye gitme ihtimalini ne kadar artırdığını gösterir. Yani eşik değerin hemen çevresine odaklanarak, yüksek puanlı öğrencilerin zaten üniversiteye gitme olasılığının yüksek olmasından kaynaklanan karışıklığı ortadan kaldırmış oluruz.

Eğer biz tüm puan aralığına bakarak karşılaştırma yaparsak, 60 alan öğrencilerle 95 alan öğrencileri kıyaslamak zorunda kalırız. Bu durumda farkın büyük kısmı zaten sınav başarısının üniversiteye gitme ihtimaliyle olan ilişkisini yansıtır, programın etkisini ayırmak zorlaşır.

Ama eşik değerin hemen çevresinde (örneğin 88–92 puan bandı) öğrencilerin akademik kapasitesi çok benzerdir. Tek belirleyici fark, programın uygulanıp uygulanmamasıdır. Bu nedenle eşik değere yakın karşılaştırmalar, adeta “doğal bir deney” ortamı yaratır ve programın nedensel etkisini temiz şekilde ortaya çıkarır.

Neden Eşik Değeri çevresi önemli?

Normal bir kontrol yaklaşımı, Running Variable’ın her yerdeki etkisini ayırmaya çalışır ama başka karıştırıcı yollar (örneğin W gibi bilinmeyen değişkenler) varsa yine sorun olabilir. Fakat eşik değeri çevresine odaklandığımızda, işlemin gerçekleşmesi neredeyse rastgele hale geldiği için bilinmeyen başka gizli yollar da kapanmış olur.

Aşağıdaki figür bunu gösteriyor: Running Variable yanında başka bir değişken W de Y’yi etkiliyor olabilir, ama eşik değeri çevresinde karşılaştırma yaptığımızda bu yol da kapanır ve izole edilmiş yol Treatment → Y kalır

GIF üzerinden bakalım:

Grafikte Running Variable (ör. sınav puanı) yatay eksende, Y (ör. üniversiteye gitme) dikey eksende. Eşik değeri çizgisi (dikey kesikli çizgi) eşik değerini gösteriyor. Eşik değerin solundakiler işlemi/treatment almıyor, sağındakiler alıyor. Ham veride hem Running Variable’ın hem de Treatment’in etkileri iç içe geçmiş durumda.

Running Variable’ın Y üzerindeki genel eğilimi gösteriliyor. Yani puan yükseldikçe Y de doğal olarak artıyor. Bu, programın etkisini (yani işlemi/treatment) doğrudan ayırt etmeyi zorlaştırıyor

Analiz özellikle eşik değerin hemen öncesi ve sonrasındaki gözlemlere indirgeniyor. Burada öğrenciler (ya da bireyler) neredeyse aynı Running Variable değerine sahip, tek fark eşik değerinin sağında olanların işleme maruz kalmasıdır.

Eşik değerin solundaki (Untreated) ve sağındaki (Treated) gözlemler için ayrı regresyon doğruları çiziliyor. Böylece her iki tarafta Running Variable’ın kendi trendi kontrol edilmiş oluyor.

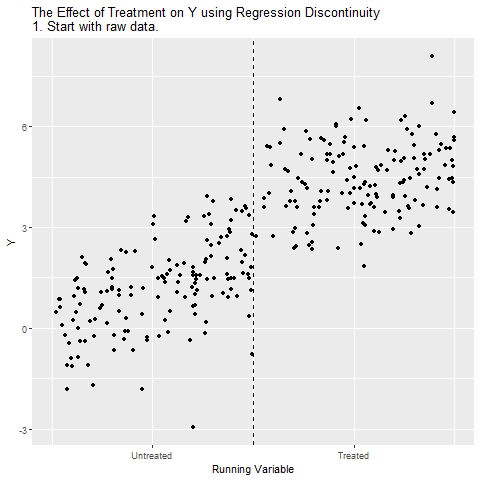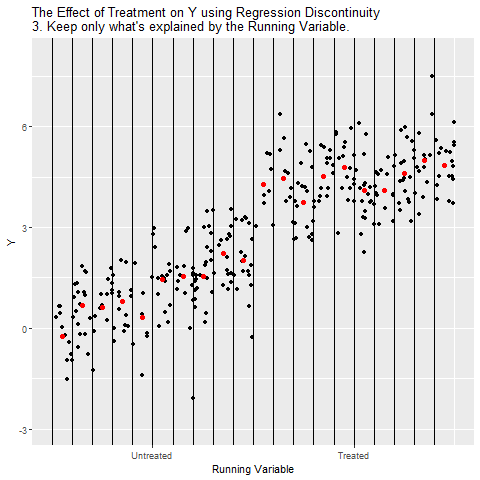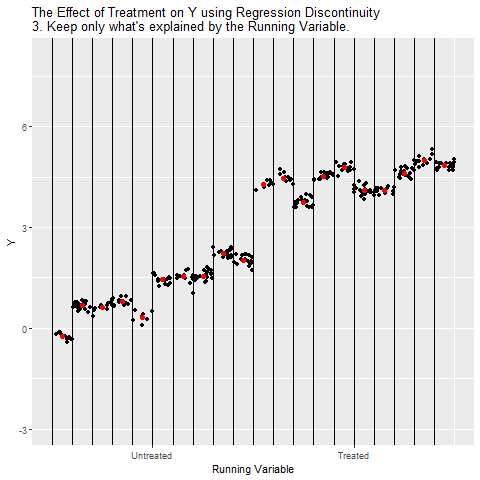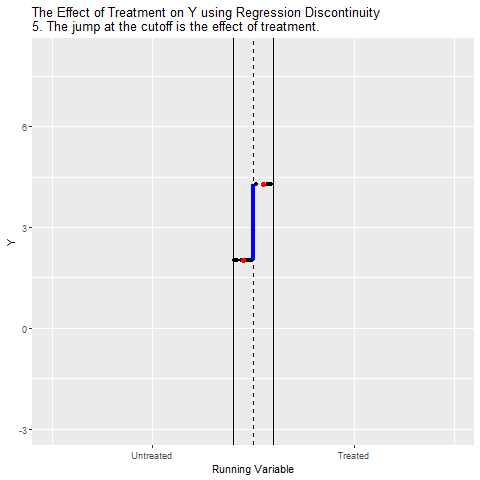
Eşik değeri çizgisinin hemen solundaki ve sağındaki regresyon doğruları arasındaki dikey fark hesaplanıyor. Bu sıçrama, Treatment’in Y üzerindeki etkisini gösteriyor.

Sonuçta RD yöntemi, Running Variable’ın genel etkisini kontrol ederek, eşik değeri çevresindeki neredeyse rastgele ayrımı kullanıyor. Böylece programın/işlemlerin nedensel etkisi izole edilmiş oluyor

Peki Ne Zaman Kontrol Uygulamak Yanlıştır?

Çarpışan Değişkenler (Collider Variables)

Değişkenleri kontrol etmek genelde faydalıdır çünkü gizli yolları kapatıp nedensel etkiyi daha doğru tahmin etmemizi sağlar ama her durumda değişkenleri kontrol etmek hatalı bir yaklaşımdır. Bazen, kontrol etmek tam tersine hatalı sonuçlara yol açar.

Aşağıdaki diyagramda gösterildiği gibi: Diyelim ki X ve Y arasında doğrudan bir ilişki yok fakat her ikisi de C isimli bir değişkeni etkiliyor. C’ye bu yüzden “collider” denir çünkü oklar C’de çarpışır:

Örnek:
Bir programlama işine başvuran adayları düşünelim.

• X = Programlama becerisi

• Y = Sosyal beceri

• C = İşe kabul edilmek

Bir adayın kabul edilmesi, programlama ve sosyal becerilerinin toplam düzeyine bağlıdır. Yani çok iyi programcı ama sosyal yönü zayıf olanlar da sosyal becerisi çok yüksek ama programlama zayıf olanlar da kabul alabilir.

Burada X ile Y’nin aslında doğrudan bir ilişkisi yok. Ama “her ikisi de C ile bağlantılı, o halde C’yi kontrol edelim” diye düşünmek yanlış olur. Çünkü:

• X → C ← Y yolu zaten kapalıdır.

• C’yi kontrol etmek bu yolu yeniden açar ve X ile Y arasında sahte bir ilişki yaratır. Sonuç olarak X ve Y aslında bağımsızken, C’yi kontrol ettiğimizde sanki ilişkiliymiş gibi görünürler. C’yi kontrol etmek yanlış sonuç çıkarılmasına neden olabilir.

Şimdi aşağıdaki GIF üzerinden bakalım:

1. Grafikte X ile Y arasındaki ilişki gösteriliyor. Başlangıçta aralarında neredeyse hiç ilişki yok (korelasyon ≈ 0). Yani X ve Y gerçekte bağımsız.

2. Veri iki renge ayrılıyor: C=0 olanlar ve C=1 olanlar. Bu, “işe alınanlar” ve “alınmayanlar” gibi düşünülebilir. C hem X’ten hem Y’den etkileniyor ama X ile Y arasında doğrudan bir bağ yok.

3. Şimdi X ve Y ilişkisine C grupları içinde bakılıyor. Bu noktada, C’nin belirleyici rolü nedeniyle her grupta X ile Y arasında yapay bir eğilim oluşmaya başlıyor.

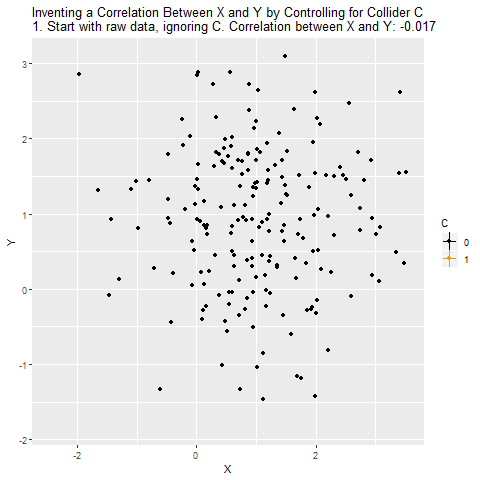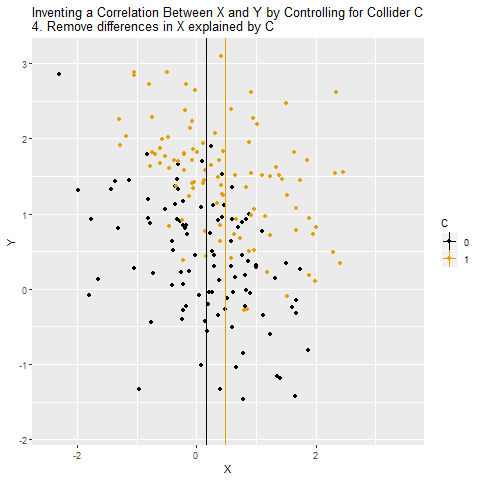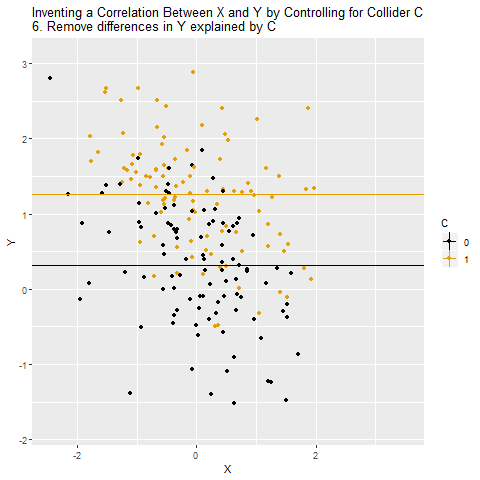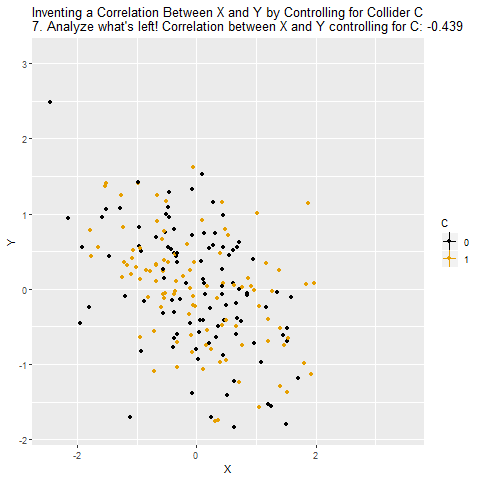
4. C’yi kontrol ettiğimizde, yani “aynı C değerine sahip bireyler arasında” X ile Y ilişkisini ölçtüğümüzde, aralarında aslında olmayan bir ilişki ortaya çıkıyor.

5. Artık X ile Y’nin bağımsız olmadığı izlenimi doğuyor. Halbuki bu ilişki gerçekte yok. Sadece C bir collider olduğu için kontrol edildiğinde kapalı yol açılmış oluyor.

Sonuç: Collider değişkenlerini modele dahil etmek yanlıştır. Başlangıçta aralarında ilişki olmayan değişkenler arasında C üzerinden sahte bir ilişki üretilir. Yani kontrol etmek bazen doğru ilişkileri göstermez; aksine hatalı nedensellik yaratır.

O Halde Karıştırıcı ve Çarpışan Değişkenler Arasındaki Fark Nedir?

Tamamen farazi bir karıştırıcı değişken (confounder)örneği düşünelim:

Diyelim ki daha fazla eğitim (X) almanın, daha yüksek siyasal katılıma (Y) (örneğin oy verme, protestoya katılma, partiye üye olma) yol açıp açmadığını araştırmak istiyoruz.

Daha yüksek eğitime sahip kişiler (X), genellikle daha yüksek gelire (Z) de sahip olurlar.

Daha yüksek gelir (Z) ise kendi başına siyasal katılımı (Y) artırır; çünkü varlıklı kişiler kampanyalara bağış yapabilir, daha fazla boş zamana sahip olabilir ya da siyasal olarak daha etkilidirler.

Burada gelir (Z) bir confounder (karıştırıcı değişken)’dir:

• Maruziyetle (eğitim) ilişkilidir.

• Sonuç üzerinde (siyasal katılım) bağımsız bir etkisi vardır.

Çarpışan Değişken (Collider Örneği)

Eğitim düzeyi (X) ile aile geliri (Y) arasındaki ilişkiye bakıyoruz.

Genel olarak toplumda eğitim ile gelir arasında bir ilişki olabilir ama diyelim ki biz özellikle başarılı/çok iyi bir özel üniversiteye kabul edilen öğrencileri (C) inceliyoruz.

• Başarılı/çok iyi bir özel üniversiteye kabul edilmek hem aile gelirinden hem de bireysel eğitim başarısından etkilenir:

• Çok yüksek gelirli ama orta seviyede akademik başarısı olan öğrenciler de girebilir (burssuz).

• Çok düşük gelirli ama olağanüstü akademik başarısı olan öğrenciler de girebilir (burslu).

Ama ortalama seviyede hem geliri hem de başarısı olanlar genelde giremez.

Sonuç olarak eğer sadece “çok iyi bir özel üniversiteye kabul edilenler”i (yani collider olan C’yi) incelersek, eğitim başarısı ile aile geliri arasında negatif bir ilişki görebiliriz. Halbuki toplum genelinde böyle bir ters ilişki yoktur; tam tersine, pozitif bile olabilir.

İşlem Sonrası Değişkenleri Kontrol Etmek (Post-Treatment Controls)

Değişkenleri kontrol edip gizli yolları kapatarak nedensel bir etkiyi ortaya çıkarabileceğimiz için, elimizden gelen her şeyi kontrol etmenin iyi bir fikir olduğunu düşünebiliriz. Ama durum her zaman böyle değildir, bazen bir şeyi kontrol etmek kötü sonuçlar doğurabilir.

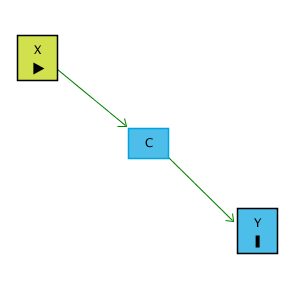
Örneğin, X’in Y üzerinde bir etkisi olduğunu düşündüğümüz bir durum olsun. Fakat X’in Y üzerindeki etkisi aslında X’in C üzerindeki etkisinden, C’nin de Y üzerindeki etkisinden kaynaklanmaktadır. C’ye post-treatment diyoruz çünkü etkisini bilmek istediğimiz değişken olan X’ten etkilenmektedir.

Örnek:

• X = Sigara Fiyatı

• C = İçilen Sigara Sayısı

• Y = Sağlık Durumu

Sigara fiyatı, sağlık durumunu sadece içilen sigara sayısını azaltarak etkiler. Yani X’in Y’ye etkisi tamamen C üzerinden geçer. Eğer “C de Y’yi etkiliyor” diye düşünüp C’yi kontrol edersek hata yaparız. Çünkü C, kapatmamız gereken bir gizli yol üzerinde değildir. Aksine, X → C → Y asıl görmek istediğimiz yolun kendisidir. C’yi kontrol etmek bu yolu keser ve X’in Y üzerinde etkisi yokmuş gibi görünmesine neden olur. Bu durumu gösterir: Kontrol ettiğimizde, gerçek etkiyi yanlışlıkla ortadan kaldırırız.

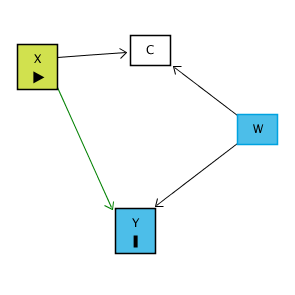
İşlem Sonrası Değişkenler sadece Y’yi etkilediklerinde sorun çıkarmaz. Başka şekillerde de problem yaratabilirler. Örneğin:

• C, X’ten etkileniyor.

• Ama C aynı zamanda W ile bağlantılı.

• W, Y üzerinde de etkili.

Bu durumda X → C ← W → Y gibi bir yol vardır. Normalde bu yol kapalıdır, yani sorun yoktur. Ama eğer C’yi kontrol edersek, collider yolu açılır ve X ile Y arasında sahte bir ilişki ortaya çıkar. Örneğin aşağıdaki gibi:

Sonuç olarak işlem sonrası (post-treatment) değişkenleri kontrol etmek, ya asıl nedensel yolu kapatır (X → C → Y yolunu siler) ya da collider etkisi üzerinden sahte ilişkiler yaratır. Bu nedenle analizde hangi değişkenin gerçekten kontrol edilmesi gerektiği çok dikkatli seçilmelidir.

Aşağıdaki GIF üzerinden inceleyelim:

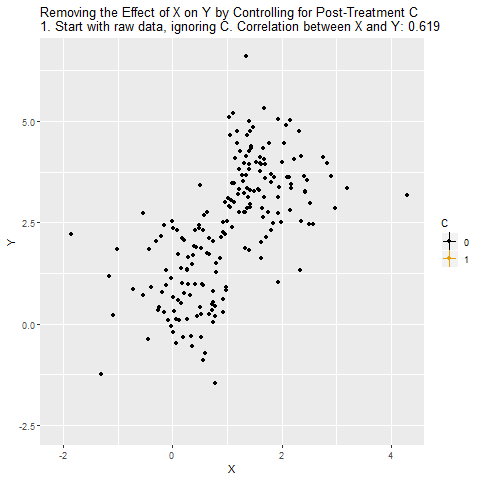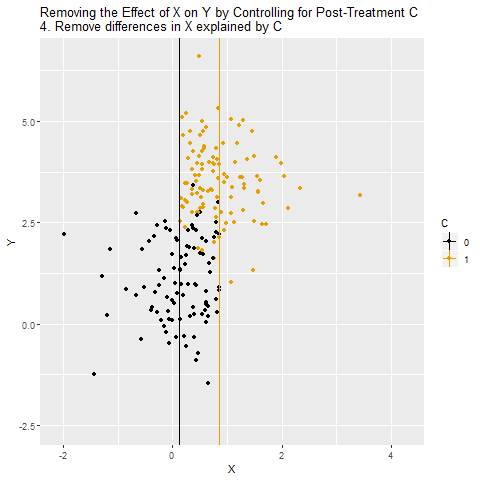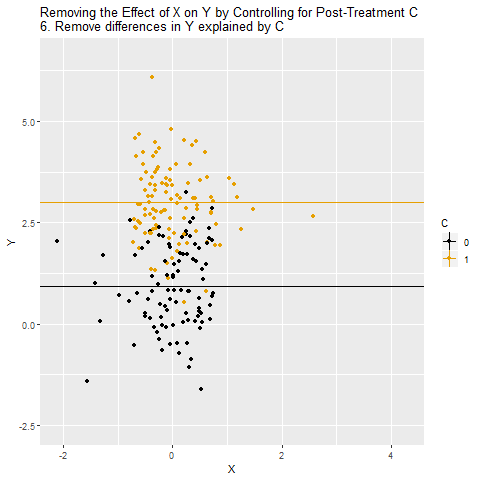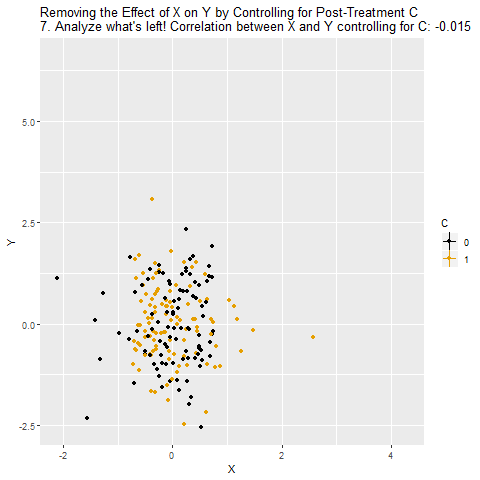
Grafikte X ile Y arasındaki ilişki görülüyor. Korelasyon oldukça yüksek (örneğin 0.619). Burada X, Y’yi C üzerinden etkiliyor: X → C → Y.

C’nin hem X’ten etkilendiği hem de Y üzerinde etkili olduğu gösteriliyor. C, aslında X ile Y arasındaki nedensel yolun tam ortasında.

Veri noktaları C=0 ve C=1 olacak şekilde ayrılıyor. Bu, C’nin X ve Y arasındaki ilişkiyi nasıl taşıdığını görselleştiriyor.

C sabitlenmiş gibi düşünülerek X ile Y arasındaki ilişki ölçülüyor. Ama burada büyük bir sorun var: C, aslında kapatmamız gereken bir gizli yol değil, asıl yolun kendisi.

C’yi kontrol ettiğimizde, X ile Y arasındaki nedensel etki “kapatılmış” oluyor. Çünkü X’in Y üzerindeki etkisi zaten C üzerinden geçiyordu. Dolayısıyla sanki X ile Y arasında hiçbir ilişki yokmuş gibi görünüyor.